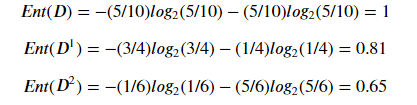一、引入

我们知道，决策树最终的优化目标是使得所有叶节点的总不纯度最低，即对应衡量不纯度的指标最低，但是目前并没有一种简单高效的方法来获得全局最优的树，因此，我们仍然要以局部最优的方法来完成决策树的建模。具体来讲，就是通过优化条件的设置，使得在每一步划分都是局部最优的条件下尽可能的达到全局最优结果。

那么，问题来了，如何设置优化条件呢？这就涉及到了我们之前所学的信息熵，即在进行节点划分时，尽可能选取使得该节点对应的子节点的信息熵最小的属性。也就是说，希望通过该属性的划分使得父节点信息熵与子节点总信息熵之差达到最大。这意味着使用该属性进行划分所获得的 "不纯度提升" 越大。因此，我们引入了“信息增益”的概念。

二、信息增益的概念

（1）条件熵
在讲解信息增益之前，我们先来补充一下条件熵的概念，在理解熵的基础上，条件熵是指在给的某个条件后信息的不确定程度。依据前面的例子，的熵可以计算出来，现增加条件，那么，在已知条件的情况下计算出来的的信息熵就称之为是条件熵。

（2）信息增益
用的熵减去在条件下的熵就是信息增益。简单来讲，信息增益就是熵减去条件熵，表示在给定条件下，信息不确定性的减少程度，也可以说是由节点划分而带来的数据纯度的提高、复杂度的下降。信息增益越大，说明节点划分后数据不确定性减小的越多，分类的效果越明显。

假设离散属性 有 个可能的取值，那么，使用属性 进行节点划分时就会产生 个节点，此时，信息增益的具体的计算可以表示为：

其中， 表示父节点的记录数， 表示属性 的取值个数， 表示数据集中所有在属性 上取值为 的记录数。

（3）举例说明

假设 表示年龄小于15的时候有5人打游戏，5人不打游戏。其中，在性别为男性的分支下，有3人打游戏，1人不打游戏。在性别为非男性的分支下，有1人打游戏，5人不打游戏， 代表节点的属性年龄小于15。

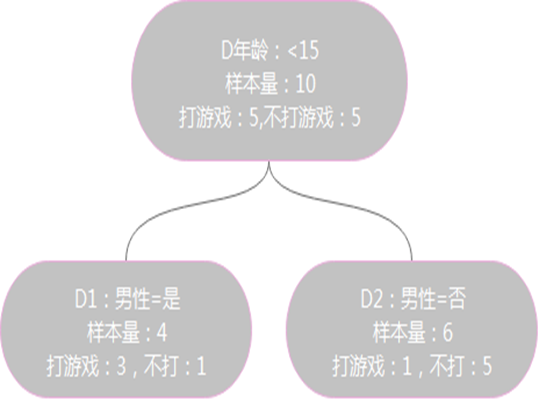
根据上述例子，我们可以计算 作为节点的信息增益为：

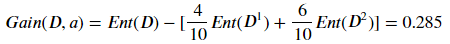
其中：